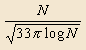|
Maris-McGwire-Sosa
Numbers
Or, Mathematics Plays
Baseball (again) |
Introduction
Consider the pair of consecutive integers 273 and 274. For each number, sum up all the decimal digits in its prime factors and in the number itself, like so:
273 = 3 x 7 x 13 and (2 + 7 + 3) + (3 + 7 + 1 + 3) = 26 274 = 2 x 137 (2 + 7 + 4) + (2 + 1 + 3 + 7) = 26
We find that the two sums are equal! We call a pair of integers (n, n+1) a Maris-McGwire-Sosa pair if they share this property. Given our choice of nomenclature, it will not be surprising to learn that
61 and 62 are a Maris-McGwire-Sosa pair
in honor of the 62nd season home run hit by Mark McGwire on 8 Sept 1998 and Sammy Sosa on 13 Sept 1998, which eclipsed the long-held record of 61 by Roger Maris. Note the similarity of our definition to the now-famous concept of Ruth-Aaron pairs [1], in which the sum of the prime factors of n and n+1 are equal. (Of course, 714 and 715 are a Ruth-Aaron pair.)
We refer to n in the pair (n, n+1) as a Maris-McGwire-Sosa number (or MMS number for short). Here are all the MMS numbers less than 1000:
7 14 43 50 61 63 67 80 84 118 122 134 137 163 196 212 213 224 241 273 274 277 279 283 351 352 373 375 390 398 421 457 462 474 475 489 495 510 516 523 526 537 547 555 558 577 584 590 592 616 638 644 660 673 687 691 731 732 743 756 774 787 797 860 871 878 895 907 922 928 944 949 953 965 985 997
Is it possible for three consecutive integers to have equal sums in this way? The answer is yes, as indicated by the appearance of some consecutive integers in the table above. (212, 213, 214) is the smallest MMS triplet, since
212 = 2 x 2 x 53 and (2 + 1 + 2) + (2 + 2 + 5 + 3) = 17 213 = 3 x 71 (2 + 1 + 3) + (3 + 7 + 1) = 17 214 = 2 x 107 (2 + 1 + 4) + (2 + 1 + 0 + 7) = 17
In the remainder of this article we explore some questions related to MMS pairs and higher MMS k-tuples (sets of k consecutive integers with equal sums).
Some Numerical Results
We used a computer to find all MMS k-tuples (with all values of k > 2) less than 109. Here is an inventory of the number of each type that were found:
| 32023033 | pairs |
| 1258453 | triplets |
| 53143 | 4-tuples |
| 2243 | 5-tuples |
| 92 | 6-tuples |
| 2 | 7-tuples |
(In this inventory we only count k-tuples that are not also r-tuples for r>k.)
Of particular interest is the smallest integer that begins an MMS k-tuple, for each value of k. The first six elements of this sequence are:
7, 212, 8126, 241995, 1330820, 1330820, ...
Note that the first 6-tuple occurs at the same place as the first 7-tuple; indeed, the occurrence of a 7-tuple as early as 1330820 seems quite remarkable; we shall have more to say on this later. (The first 6-tuple that is not part of a 7-tuple occurs at 3539990.)
For which k values do Maris-McGwire-Sosa k-tuples exist? It seems reasonable to conjecture that as we examine more and more integers we will eventually find a k-tuple for any value of k (or at least for arbitrarily large values of k), but a proof of this seems difficult.
Here are the first few MMS k-tuples, for k=3 to 9. Only the first number in each k-tuple is shown:
| Value of k | Initial Maris-McGwire-Sosa k-tuples |
| 3 4 5 6 7 8 9 |
212, 273, 351, 474, 731, 1247, 1296, 1634, 1988, ... 8126, 16657, 16675, 19665, 23714, 41885, 49449, ... 241995, 349856, 694746, 797181, 1330820, ... 1330820, 1330821, 3539990, 19415425, 20976927, ... 1330820, 829885449, 3249880870, 3249880871, ... 3249880870, 3249880871, 12222533493, ... 3249880870, ... |
We also define m(k) as the smallest integer that begins a run of exactly k (and no more than k) consecutive integers that are MMS numbers. That is, m(k) is the index of the smallest MMS k-tuple that is not also an r-tuple for any r > k. The initial terms of the sequence of m(k) values (the first six calculated by the author, the last two by Hans Haverman) are:
7, 212, 8126, 241995, 3539990, 1330820, 12222533493, 3249880870, ...
We now turn our attention to the question: how are the MMS k-tuples distributed among the integers?
An Asympotic Estimate
We wish to estimate the number of integers less than 10m that are Maris-McGwire-Sosa numbers. Let n be such an integer with m digits. For n to be a MMS number, we must have
s(n) + p(n) = s(n+1) + p(n+1), or
p(n+1) - p(n) = s(n+1) - s(n)
where s(n) is the sum of the digits in n and p(n) is the sum of the digits in the prime factors of n. But since n and n+1 are consecutive, s(n+1) - s(n) equals 1 (9/10 of the time: whenever n = 0 to 8 mod 10) or 8 (9/100 of the time: when n is not equal to 99 mod 100), etc. So we must have
p(n+1) = p(n) + (1 or 8 or ...)
Now, since n has m digits, so does (asymptotically) its collection of prime factors, since their product equals n. The digits in the prime factors of n can (roughly speaking) be considered to be uniformly distributed random digits. Therefore, the above equation can be modelled by the following problem. Throw two sets of m identical 10-sided dice. What is the probability that the two sums differ by exactly 1 or 8 or ...?
A well-known theorem from probability states that the probability distribution of the sum of m copies of X, where X is a uniform distribution over {0....t} with squared variance s2, is approximately P(x) = N(x/a) / a, where N is the standardized normal distribution with mean 0 and variance 1, and
a = (ms2)1/2
This corresponds exactly to our dice-throwing problem, since we have the set {0...9}, with s2 = 33/4. Asymptotically, the extra "1 or 8 or ..." term can be set to zero, and we just calculate the probability that the two sets of m dice give the same sum. This has probability distribution function P2(x). The total probability of a matching sum is the integral of P2(x). Thus,
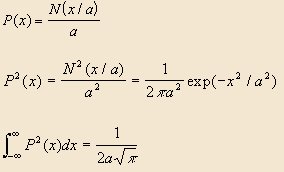
Now, substituting
a = (ms2)1/2,
and
s2 = 33/4,
leads to our main result:
Conjecture 1: The probability of an integer less than 10m being an MMS number is approximately
(1)
As a consequence, we have:
Corollary: The expected number of MMS pairs less than N is roughly
(2)
This formula predicts 57 MMS pairs less than 1000 (as compared with the 76 shown above), and becomes even more accurate as N gets larger. For example, it gives 40095 for N=107 (exact number: 44304) and 32737600 for N=109 (exact number: 34668812).
If conjecture (1) is correct, the asympotic density of MMS pairs is zero. However, note that the presence of both a square root and a log in the denominator of (2) means that they "thin out" very slowly. For example, in the vicinity of 101000 we still expect to find a MMS number about once every 100000 integers.
How many MMS k-tuples are there, asymptotically? A simple estimate can be obtained by considering the probability of an MMS 3-tuple to be the same as the probability of two independent 2-tuples, and hence equal to the value of (1) squared (and similarly for higher k-tuples). For example, this predicts 512 4-tuples less than 107 (exact number: 909).
The frequency of appearance of MMS k-tuples serves to emphasize the remarkable nature of the 7-tuple that appears at 1330820. The statistics tell us that we should not expect the first 7-tuple until about 109, whereas it actually occurs around 106! Here is this very noteworthy sequence of seven integers:
1330820 = 2 x 2 x 5 x 66541 (1+3+3+0+8+2+0) + (2+2+5+6+6+5+4+1) = 48 1330821 = 3 x 3 x 67 x 2207 (1+3+3+0+8+2+1) + (3+3+6+7+2+2+0+7) = 48 1330822 = 2 x 83 x 8017 (1+3+3+0+8+2+2) + (2+8+3+8+0+1+7) = 48 1330823 = 13 x 167 x 613 (1+3+3+0+8+2+3) + (1+3+1+6+7+6+1+3) = 48 1330824 = 2x2x2x3x11x71x71 (1+3+3+0+8+2+4) + (2+2+2+3+1+1+7+1+7+1) = 48 1330825 = 5 x 5 x 53233 (1+3+3+0+8+2+5) + (5+5+5+3+2+3+3) = 48 1330826 = 2 x 7 x 23 x 4133 (1+3+3+0+8+2+6) + (2+7+2+3+4+1+3+3) = 48
In closing, we remark that with modern factorization methods (see [2]) it is easy to find large MMS pairs by searching a small neighborhood or examining successive integers of a certain type. We used the elliptic curve factorization method to find the following example in just a few seconds of computer time: 12345678901234567890123456 is a Maris-McGwire-Sosa number, since
12345678901234567890123456 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 17 x 71 x 218107 x 244251294564157
12345678901234567890123457 = 211 x 15887 x 3682905932280190901
and in both cases the sum of all the digits is 222.
References
[1] Nelson, Carol, David E. Penney, and Carl Pomerance, "714 and 715", Journal of Recreational Mathematics, Vol. 7, No. 2 (1974), p. 87-89.
[2] Riesel, H., Prime Numbers and Computer Methods for Factorization, Birkhauser, Boston, 1994.