 |
The Prime Queen
Attacking Problem
Problem by G. L. Honaker, Jr. |
This interesting problem was posed by G. L. Honaker, Jr. in November of 1998. First, create any knight's tour on an n x n chessboard, in which the knight starts on some square of the board and by successive knight's moves visits every square on the board exactly once. Number the squares visited by the knight in order starting with 1 for the starting square. When you are done, place a chess Queen on any square and count the number of prime numbers attacked by the Queen (note that the Queen is not considered to be attacking the square it sits on).
Now, the problem: What is the largest number of primes that can be attacked by the Queen, for any placement of the Queen and any knight's tour?
First, note that there are 18 primes between 1 and 64. Amazingly, there is a perfect knight's tour in which all 18 primes can be attacked! Here is the first perfect solution ever constructed (by Mike Keith, in Nov. 1998):
37 24 45 4 39 22 47 62 44 5 38 23 46 61 40 21 25 36 43 60 3 20 63 48 6 59 26 35 64 41 2 19 27 30 57 42 1 34 49 12 58 7 54 29 52 13 18 15 31 28 9 56 33 16 11 50 8 55 32 53 10 51 14 17
where the location of the Queen is in blue and the attacked primes are shown in red.
Knights tours are impossible on 1x1, 2x2, 3x3, 4x4 boards, but it is natural to ask the same question for any n x n board with n > 5. Denote by Q(n) the number of attacked primes in the best known solution for a given n, and let Pr(n) be the number of primes between 1 and n2 (i.e., the number of primes on the board). Obviously, Q(n) ≤ Pr(n); if Q(n) = Pr(n) we say that n has a perfect solution, in which all the primes in the grid are attacked.
The table below shows the best known (largest) values of Q(n) for n up to 12. The bold underlined values are perfect solutions, with all primes in the grid being attacked. The last two values of Q(n) are still the best known to me, but it seems plausible that they could be improved.
| n | Q(n) | Pr(n) | Discoverer | ||
| 5 | 9 | 9 | Mike Keith, 1998 | ||
| 6 | 11 | 11 | Mike Keith, 1998 | ||
| 7 | 15 | 15 | Mike Keith, 1998 | ||
| 8 | 18 | 18 | Mike Keith, 1998 | ||
| 9 | 22 | 22 | Jacques Tramu, 2004 | ||
| 10 | 25 | 25 | Jacques Tramu, 2004 | ||
| 11 | 24 | 30 | Jacques Tramu, 2004 | ||
| 12 | 25 | 34 | Jacques Tramu, 2004 |
Here are perfect solutions for n=5, 6, 7, 9 and 10 (n=8 is shown above, of course):
5x5 board - 9 of 9 primes
3 14 19 24 1 20 9 2 13 18 15 4 25 8 23 10 21 6 17 12 5 16 11 22 76x6 board - 11 of 11 primes
1 36 15 26 3 6 16 27 2 5 34 25 11 14 35 28 7 4 20 17 12 31 24 33 13 10 19 22 29 8 18 21 30 9 32 237x7 board - 15 of 15 primes
47 12 39 8 27 14 29 38 9 46 13 30 7 26 45 48 11 40 25 28 15 10 37 2 49 16 31 6 1 44 17 34 41 24 21 36 3 42 19 22 5 32 43 18 35 4 33 20 239x9 board - 22 of 22 primes
13 76 15 20 11 74 25 22 9 16 19 12 75 26 21 10 67 24 77 14 17 28 73 56 23 8 69 18 81 78 43 60 27 68 57 66 79 44 29 2 55 72 59 70 7 30 51 80 61 42 3 36 65 58 45 48 41 52 1 54 71 6 35 50 31 46 39 62 33 4 37 64 47 40 49 32 53 38 63 34 510x10 board - 25 of 25 primes
62 21 60 75 64 87 84 77 80 89 19 24 63 86 59 76 65 88 83 78 22 61 20 01 74 85 58 79 90 81 25 18 23 46 43 66 73 82 57 54 36 39 44 67 02 47 42 55 94 91 17 26 37 40 45 72 03 92 53 56 38 35 70 11 68 41 48 95 04 93 27 16 29 32 71 12 07 52 99 96 34 31 14 69 10 49 98 05 08 51 15 28 33 30 13 06 09 50 97 00 ("00" = 100)
Is there a simple reason why perfect solutions haven't been found for n > 10? The answer is yes:
Theorem: Perfect solutions are impossible when n ≥ 11.
Proof: First, color the board's squares white and black in the usual way (as on a chessboard). Now notice that, due to the properties of the knight's move and the numbering of the tour with successive integers, all black squares (or white squares) on the board have numbers with the same parity (odd or even). Note that all the prime numbers we want the queen to attack are odd numbers, with one exception (the even number 2). Define M(n) as the maximum number of primes that could possibly be attacked by a queen given these parity considerations. This is simply the maximum number of odd numbers we could attack plus one (for the prime 2, which doesn't have to use up one of the odd-number slots). Note that the queen itself will also be located on an odd-numbered square.
Without loss of generality we can put the odd numbers on the black squares, then find the best black square to put the queen on to attack as many black squares as possible, and count how many are attacked. In the diagrams below, each X is a black square attacked by the queen (Q) diagonally, while O is a black square attacked orthogonally. Let X(n) and O(n) represent the number of X's and O's for a given n. It turns out that there are four cases for the X(n) and O(n) values based on the value of n mod 4. These four cases are illustrated by the boards for n = 8, 9, 10, and 11, though the formulas work for any n.
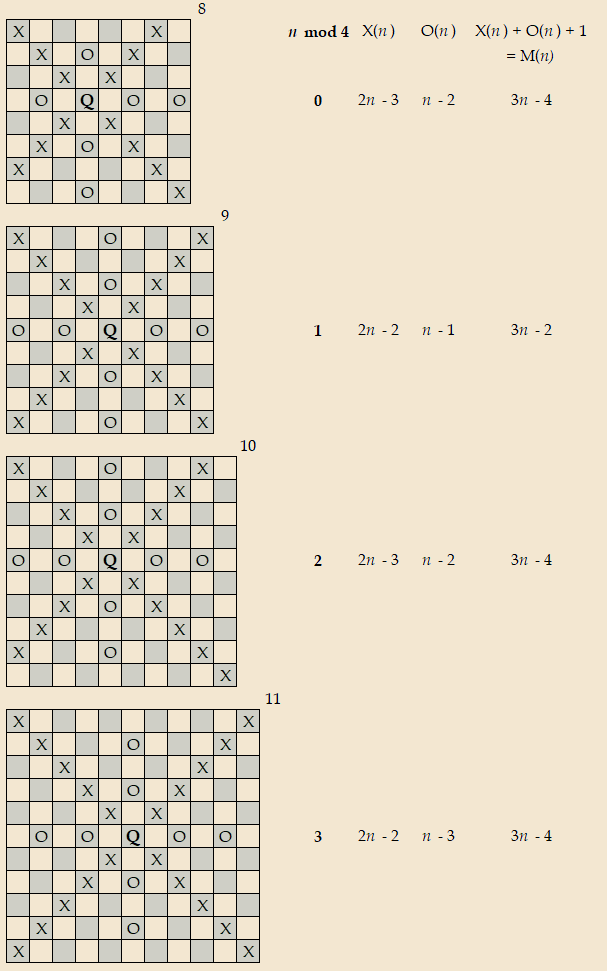
Using the values of X(n) and O(n) given by these diagrams, then computing M(n) = X(n) + O(n) + 1 (again, the +1 comes from the fact that we also attack the even prime 2), the answer simplifies to
M(n) = 3n - 2 if (n mod 4) = 1
3n - 4 otherwise
If M(n) < Pr(n) a perfect solution is impossible, since the maximum number of primes we can possibly attack is less than the number of primes we need to attack. Here are the first few values of M(n) and Pr(n) starting at n = 5:
n 5 6 7 8 9 10 11 12 13 14 15 M(n) 13 14 17 20 25 26 29 32 37 38 41 Pr(n) 9 11 15 18 22 25 30 34 39 44 48
As indicated by the red numbers, from n = 11 onward M(n) is less than Pr(n). This will continue for larger n, since M(n) grows linearly (it is basically 3n) while Pr(n) has a growth rate of n2/log(n), which is faster than linear. This completes the proof.
A harder version of this problem requires the knight's tour to be closed (reentrant), which means that the last square in the knight's tour is a knight's move away from the first square. In April 1999, "qscgz" (Guenter Stertenbrink) found the first perfect reentrant 8x8 solution:
19 58 33 6 21 16 13 8 32 5 20 17 34 7 22 15 57 18 59 4 29 14 9 12 42 31 56 35 62 11 28 23 55 60 43 30 3 24 63 10 44 41 46 61 36 27 50 25 47 54 39 2 49 52 37 64 40 45 48 53 38 1 26 51
Some other intriguing questions include:
(1) Are the Q(n)
values for n=11, and 12 shown above really the best possible?
If they can be improved, how close can we get to M(n)?
What about even larger n?
(2) Can a closed tour always be found that attacks as many primes as the
best open tour on the
same board?
(3) Generalize to an n x m board and determine the values of
Q(n, m). For which (n, m) values are there perfect solutions?
(4) What are the best solutions using other chess pieces,
or pieces from chess variants, instead of the queen?
In closing, here is another interesting solution sent to me by George Jelliss. Consider the following 8x8 re-entrant tour, with the queen on 1:
4 7 10 23 64 19 12 15 9 24 5 18 11 14 63 20 6 3 8 1 22 61 16 13 25 30 37 60 17 50 21 62 36 59 2 29 42 53 46 51 31 26 33 38 49 40 43 54 58 35 28 41 56 45 52 47 27 32 57 34 39 48 55 44
Although the queen on square 1 only attacks 17 of the 18 primes, this tour has a property not present in any of the 18-attacking tours above, which is that all 17 odd primes are attacked, and every odd number attacked by the queen is a prime.